5.1. ASPECT CINEMATIQUE
C'est la loi de mouvement (ou équation de mouvement)
que l'on désire qui détermine le profil de la came. Le cahier des charges prévoit en général que l'on
doit faire un mouvement d'une amplitude "x" en une durée "t",
l'amplitude pouvant être un déplacement linéaire (le suiveur se translate) ou angulaire (le suiveur est sur pivot). Cela
doit se faire en limitant :
|
|
la vitesse : un mouvement rapide implique une consommation d'énergie importante (Ec =
(1/2)mv², l'énergie cinétique croît selon la vitesse au carré),
un échauffement (par frottement) et une usure des guidages (rails, galets,
paliers) ;
l'accélération : une accélération importante implique des efforts importants (selon le principe fondamental de la dynamique
) et donc des déformations et des contraintes élevées ;
Or les pièces sont soumises à une vitesse de rotation wr et
une accélération ar qui doivent être respectivement inferieurs à la vitesse de retour
du suiveur qui lui est soumis soit à son propre poids "P" ou à un ressort de raideur "k".
Ainsi on peut noter que ar < P ou dans le cas d'un ressort ar
< k.
Ainsi cette inéquation permet d'éviter les sauts du suiveur sur la came et cela lui permet de rester constamment en contact avec
celle-ci. Autrement dit il faut adapter la raideur du ressort de retour du suiveur à la vitesse de rotation de la came.
Les à-coups doivent aussi être pris en compte car c'est une source d'usure et de bruit ainsi que la forme imparfaite de la came et ou du
suiveur..
Les principales fonctions utilisées pour les rampes des cames
|
 |
5.1.1. Vitesse de glissement d'une came
Par définition la vitesse de glissement au point de contact "A" came (1)/galet (2)
(ou pièce)est la vitesse relative VA1/2.
Elle est caractérisée par le vecteur vitesse relative VA1/2 tangente à l'instant "t
" du point "A" avec la surface considérée, par rapport à laquelle s'effectue le glissement de ce point.
VA2/0: Vitesse axiale de la pièce 2.
VA1/0: Vitesse linéaire ou tangentielle de la pièce 1.
en A: VA1/0 = VA1/2 + VA2/0
|
|
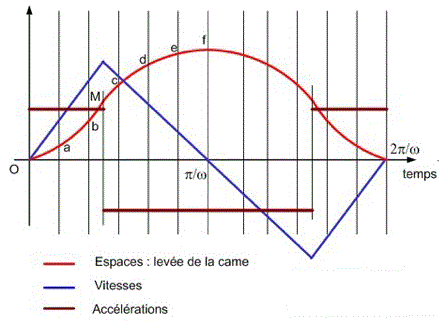
5.1.2. Courbe des espaces: e=f(t)
Elle traduit l'étude des levées en fonction de l'angle balayé téta "q" ou mieux en fonction du temps "t".
On peut en déduire:
a) la courbe des vitesses v=f(t) qui donne la tangente à
la courbe des espaces
b) La courbe des accélérations a=f(t) qui donne la tangente à la courbe des vitesses.
c) la valeur de l'inertie "ma".
Une période correspond à un tour complet de l'arbre porte came. |
 |
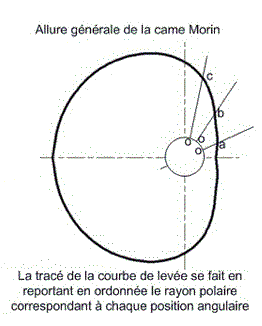
5.1.3. Profil théorique de la came:
C'est le lieu des positions successives du centre du galet. Il est décrit par son cercle de levée nulle, de rayon minimum R
a) Cercle de levée nulle, rayon minimum "R".
R = Rmoyeu + rgalet
b) A chaque division de la période 1/4, 1/8, 1/12 au choix correspond un espace "E"
E= e + Rmoyeu + rgalet
avec "e" l'espace pris sur la courbe des espaces pour la même décision.
et le moyeu, la pièce centrale sur laquelle tournent les objets.
Plus le rayon "R" de la came à disque est grand selon l'angle "q
" alors, plus l'amplitude sera élevée au point correspondant.
Ainsi, en modifiant la came, on peut obtenir nimporte quel tracé de courbe périodique.
Il existe ainsi des spécifiques aux courbes sinusoïdales
|
|


